乗法 公式 問題 878883

 乗法公式については展開後の形を暗記することが一番良いです。 ① (x a)(x b) = x^2 (a b)x ab ② (x a)^2 = x^2 2ax a^2 ③ (x a)^2 = x^2 2ax a^2 ④ (x a)(x a) = x^2 a^2 ①の公式はこの後の因数分解でもよく使いますので、丸暗記してしまいましょう。中3 数学の基本問題 中3 式の計算 単項式と多項式の乗除 PDF 答え付き 多項式の乗法 （ab) (cd) PDF 答え付き 展開 乗法の公式 1 (xa) (xb) PDF 答え付き展開(乗法公式1) 次の式を計算しなさい (x1)(x2) (x3)(x5) (x4)(x6) (x7)(x1) (x4)(x7) (x2)(x8) 次の式を計算しなさい (x1) 2 (a5) 2 (x10) 2 (x2) 2 (x3) 2 (x4) 2 次の式を計算しなさい (x1)(x1) (x11)(x11) (x7)(x7) (x8)(x8)

三乗の公式 展開と因数分解 高校生向け受験応援メディア 受験のミカタ

乗法 公式 問題

乗法 公式 問題-乗法公式の問題 乗法公式を用いて下記の問題を解きましょう。 乗法公式を思い出してくださいね。展開した結果を下記に示します。 乗法公式を暗記しなくても、分配法則を理解すれば解けます。ただ、乗法公式を暗記した方が、断然、「解くスピード」が ②乗法公式で解く問題は、数が複雑になったり大きくなっても公式に当てはめれば解ける ③場合によってはaやbなどの数に置き換えてから乗法公式で計算し、計算したら元の数に置き換えなおす 以上が複雑な展開の問題を解くときのポイントです。

中３数学12 式の計算２ 乗法公式１ 標準問題 ヒント 302

2/8 乗法公式と式の展開（2分52秒） 3/8 Step1 新しい乗法公式とたすきがけ（3分51秒） 4/8 Step2 たすきがけによる因数分解（1分58秒）練習問題1 以下の式を、乗法の公式を用いて展開しなさい。 1 （ x ＋3）（ x ＋4） 2 （ x －3）（ x ＋4） 3 （ x ＋3）（ x －4） 4 （ x －3）（ x －4） 練習問題2 以下の式を、乗法の公式を用いて展開しなさい。Excelで作成した、乗法公式の計算練習問題のワークシートです。 F9（ファンクションキー）を押すたびに計算問題の数字が変化します。 乱数を活用しているので、毎回違うワークシートで学習することができます。 解答も同じシートに書かれています。 生徒が自分で答え合わせができるようにしてあります。 計算シートは8種類あります。 乗法公式1〜4、乗法公式

 ここは、乗法の公式で展開を練習します。 QRコードは答えのページへのリンクです。 乗法公式 1 乗法公式 1 答えつき 乗法公式 1答えのページ Tweet 登録カテゴリ 1000中学 数学 問題 乗法の公式 \((xa)(xb)=x^2(ab)xab\) すべての中学生が今より少しでも数学に魅力を感じてくれることを願いつつ，中学数学の問題を惜しみなく提供していきます。ただし、個人的にはこの「乗法公式」は、覚えなくても大丈夫。「面積図」さえ書ければ、問題 ないからです。まあ、あえて覚えるとすれば、3番くらいですかね。（3の式の形を「和と差の積」 ともいいますが。） では早速、練習問題に挑戦してみましょう。

乗法公式（展開公式）について，例題と使いこなすコツを述べながら公式19個を紹介していきます。 最初は易しいですがどんどん難しくなります。 目次 (xa) (xb) の乗法公式 2乗の乗法公式 和と差の展開公式 (axb) (cxd) の乗法公式 3乗の乗法公式 (abc)^2まったく数学的ではない、曖昧な問題です。 ですので、このような問題は高校入試では出題されません。 しかし、定期テストで出題されることはあるでしょう。 以下、出題者の意図した解答をお見せします。 解答 (1) \(71^229^2\) 式の展開 (乗法公式の利用2) 式の展開 展開後にさらに同類項をまとめなければいけない問題なので、乗法公式が定着していないと正確に解けない問題です。 乗法公式が不安に人はまずそちらが自信がつくまで練習しましょう。 つなぎ目が

中３ 展開と因数分解７ 乗法の公式 和と差の積 予習 中学数学の勉強に

中3数学 乗法の公式の定期テスト予想問題 Pikuu

多項式の乗除1 多項式の乗除2 展開のしかた⇒ 多項式の展開 (初) 多項式の展開 (1) 多項式の展開 (2) 乗法公式 (基礎)⇒ (初) (xa) (xb) (基) これで(xa)(xb)の展開公式もマスターしたね。 この乗法公式なら1瞬でとけちゃう。 たとえば、 (x 1) (x 2)っていう計算式があったとしよう。 公式で計算すれば瞬殺さ。 公式にあてはめてみると、 a = 1;乗法公式とは 式を展開するときに、次の公式がよく用いられます。 これらの公式乗法公式とよばれる公式です、 後の 因数分解 という単元でとても大切になるので、必ず覚える ようにしましょう。 覚えるためには、たくさんの問題を解くしかありません。

乗法公式による式の展開と因数分解 中学数学の多項式計算 リョースケ大学

無料 中３数学 基本解説 問題プリント 302 式の計算２ 乗法 公式１

 練習問題 ここで覚えた乗法公式、 $$(ab)^2 = a^22abb^2$$ を使った計算を練習してみましょう。 次の計算を乗法公式を使って解いてみます。 $$(2x 3)^2$$ まず、登場する数字と文字をすべて掛けましょう。 $$2x \times 3 \times 2 = 12x $$ 次に、$12x$を前と後ろの2乗乗法公式2基礎 例題 乗法公式 2乗 (x±a) 2 = x 2 ±2axa 2 和と差の積 (xa) (xa)= x 2 a 2 (例1) (x3)2 = x2 2×3x32 = x2 6x9 (例2) (x3) (x3) =x2 32 乗法公式って何？っていう場合は、以下の3つの記事をみて復習してから取り組みましょう。 乗法公式① 乗法公式② 乗法公式③ 置き換え問題とは？ (a＋b＋2)(a＋b＋3) を展開せよ。 という問題があったとします。こういった問題の解き方は2つあります。

中３の数学 乗法公式 がよく分からないですもう中間ﾃｽﾄがかなり近いので Yahoo 知恵袋

中3 数学 乗法公式 １ 無料学習プリント教材

多項式の計算 乗法の公式ー基本1 無料で使える中学学習プリント http//chugakumanabihirobanet/ 1 展開の公式ー基本 名前 次の乗法公式を完成させなさい。 (1)( a)( b) (2)( a)2 (3)( a)2 (4)( a)( a) 次の式を展開しなさい。 (1)( b)( d) (2)( 3)( 6) (3)( 5)( 9) (4)( 5)2 (4)( 7)2 (5)( 5)( 5) Y＋ Y＋ x− Y− ＋ Y＋乗法公式や因数分解を利用した数値計算問題の解き方です。 中学3年で覚えることになる展開公式や因数分解は暗記するためにあるのではありません。 いろいろな計算を楽にするためにあるので利用方法を解説しておきます。 基本問題しか そもそも乗法公式とは？ 乗法公式とは、名前のとおり「かけ算の公式」で、 （ ）のあるかけ算を展開するのに使われます 。 基本的なものは、中学校で習いましたね。 (x a)(x b) = x2 (a b)x ab ( x a) ( x b) = x 2 ( a b) x a b (a b)2 = a2 2ab b2 ( a b) 2 = a 2 2 a b b 2 (a − b)2 = a2 − 2ab b2 ( a − b) 2 = a 2 − 2 a b b 2

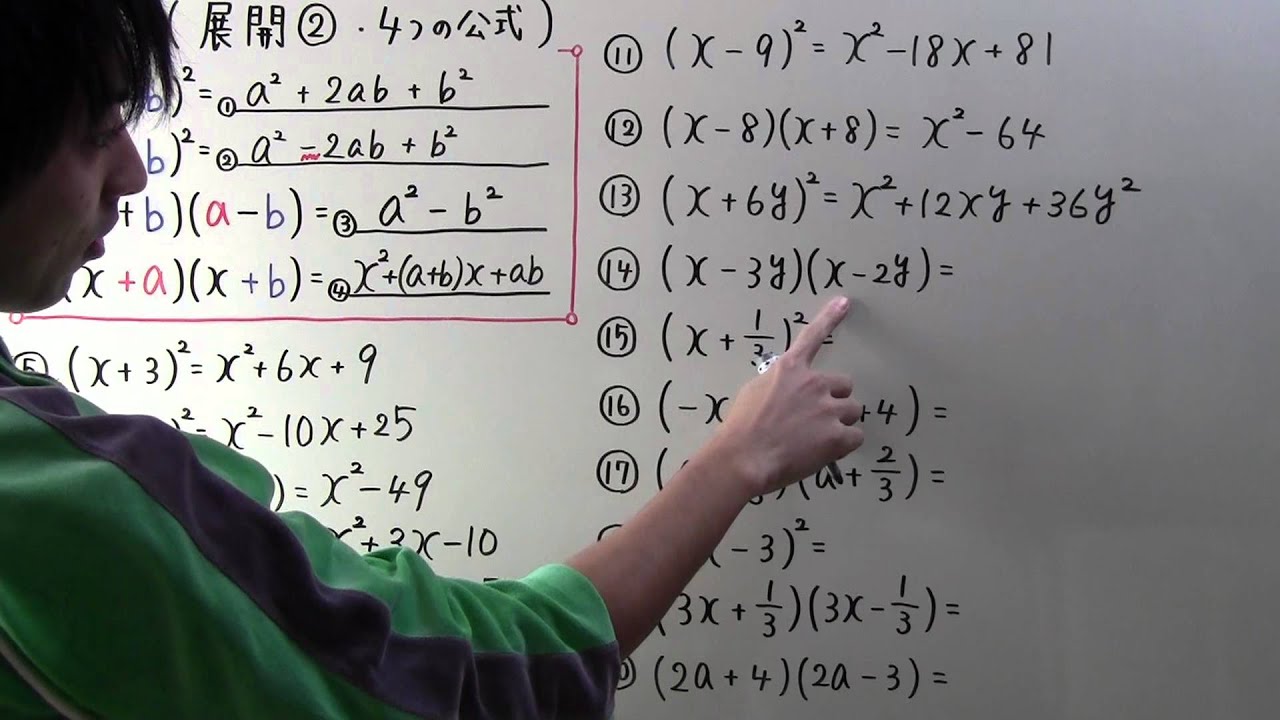
数学 中3 3 展開 4つの公式 Youtube

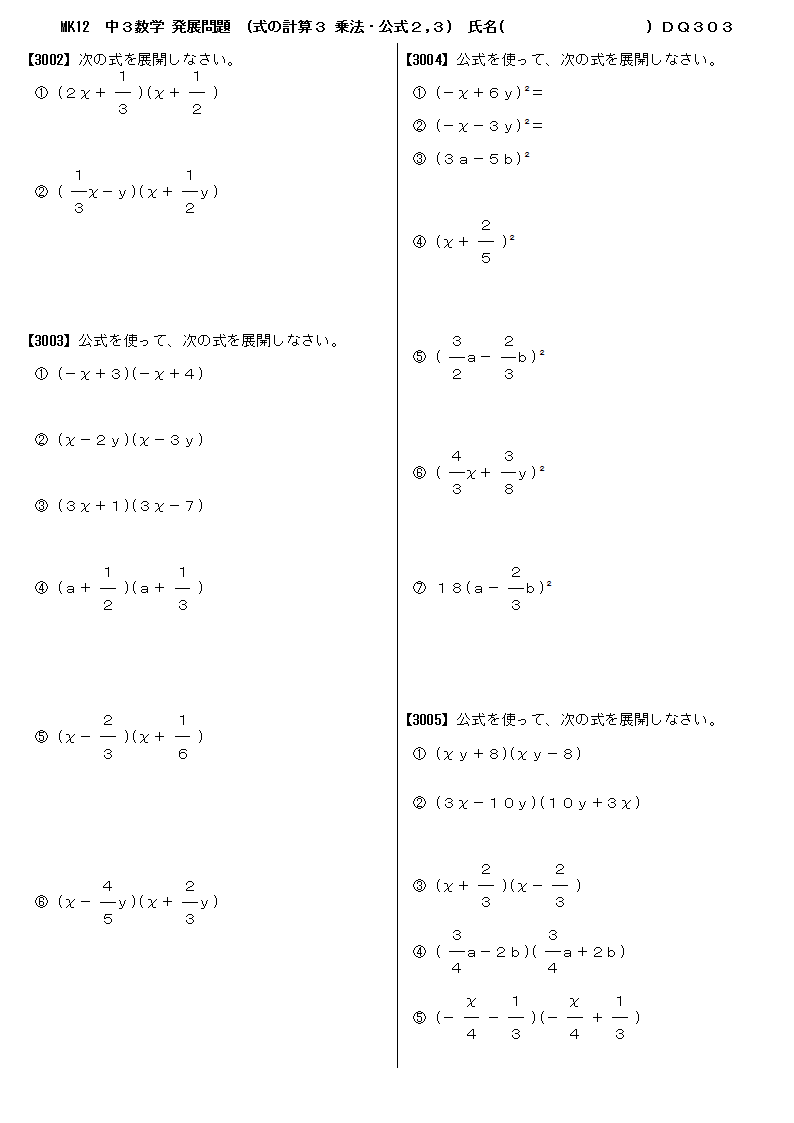
無料 中３数学 発展 応用問題 問題プリント 303 式の計算３ 乗法 公式２ ３

 今回は式の展開に使う、乗法公式の問題練習をしていきたいと思います。 式の展開で使う4つの乗法公式 中学で使う乗法公式は次の4つです。 式の展開をするときには乗法公式を用いると計算の過程が減るので時間短縮に繋がります。 4つの乗法公式を覚えるのは大変そうですが、問題練習を第1章 式の展開と因数分解 ＜前： L3 式の展開（2）‐乗法公式1 の問題 L4 式の展開（3）‐乗法公式2 の問題 ：次＞ 練習問題1 以下の式を、乗法の公式を用いて展開しなさい。 1 （ x ＋3）（ x ＋4） ＝ x 2 ＋（3＋4） x ＋（3×4） ＝ x 2 ＋7 x ＋12 2 （ x －3）（ x ＋4） ＝ x 2 ＋（－3＋4） x ＋（－3×4）高校数学の基本問題 Gogle site →数ⅠA →数ⅡB →数Ⅲ (旧C) ***最近の更新*** 反復試行の確率（入試問題） 絶対値付き関数の定積分 Rの関数hist () Rの関数sample () 名義尺度データの比率の検定 フィッシャーの正確

乗法公式 式の展開公式 19個まとめ 高校数学の美しい物語

中３数学 多項式の計算 乗法公式 因数分解 式の利用 問題編 １学期総復習１ Youtube

Nhk高校講座 数学Ⅰ 第5回 第1章 数と式 乗法公式例題の解説授業 分数式の乗法・除法の問題ですね。 まずは分数式の計算公式をおさらいしましょう。 わり算なら逆数のかけ算にする。 式が長いときは 約分するために因数分解 をして計算を進めるのがポイントでした。図形と証明 角度の求め方 角度の求め方 解説;

中3数学 乗法公式について の乗法公式 が をもとに導け Yahoo 知恵袋

1

乗法公式（1）超わかる！ 中学数学～文字式＃7乗法の公式 I © 問題プリント無料印刷学習サイト中学数学が好きになるhttps//sugakugasukicom 3 1 次の式を展開しなさい。 (1) (x3)2 (2) (3x2)2 (3) (x5y)2 (4) (x4)2 (5) (3x5)2 (6) (3x2)2 (7) (a 1 3)2 (8) (1 2 x 1 3 y)2 (9) (a04b)2 2 次の式を展開しなさい。 (1) (x−3)2 (2) (5x−1)2 (3) (6a−4b)2基本的な乗法公式（展開公式） I (ab)2=a22abb2 II (a−b)2=a2−2abb2 III (ab) (a−b)=a2−b2 ※ これらの公式のうち I～ IVは中学校の復習となっているが，高校の数学 I でもう一度出てくる．公式は中学校と同じでも，扱い方が少し変るところがある

展開の公式 乗法公式 の計算方法を図にしてみました あんず学習塾のメモ 図表置き場

数 乗法公式とその利用の定期テスト対策問題 解説付 Tekibo

だね。 すると、 (x1)(x2) = x^2 (12) x (1×2) = x^2 3x 2

U9j580gf8iba369ji2w Xyz P 565

数と式 整式の展開に関する問題を解いてみよう 日々是鍛錬 ひびこれたんれん

Www Chuogi Jp App Download E4 B8 Ad Ef 93 E6 95 B0 E5 Ad A6 80 905 E6 9c 86 E6 97 A5 80 91 Pdf T

乗法公式 時習館 ゼミナール 高等部

乗法公式

式の展開 中3のいろいろな展開問題 乗法公式を使いこなそう 中学数学をはじめから分かりやすく

乗法公式とは 1分でわかる意味 公式の覚え方 問題 因数分解との関係

中3数学 平方根 乗法公式を利用する計算問題 Youtube

高校2年 数学ii 東京書籍 1章1節 整式の乗法 除法と分数式 節末問題 解説 解答 赤城 ᐡᐤᐡ

式の展開 中3のいろいろな展開問題 乗法公式を使いこなそう 中学数学をはじめから分かりやすく

中３数学 基本問題 問題 303 式の計算３ 乗法 公式２ ３ プリント

式の展開 中3のいろいろな展開問題 乗法公式を使いこなそう 中学数学をはじめから分かりやすく

式の展開 中3のいろいろな展開問題 乗法公式を使いこなそう 中学数学をはじめから分かりやすく

乗法公式 無料で使える中学学習プリント

ルート計算 展開公式をつかう3つの平方根問題の解き方 Qikeru 学びを楽しくわかりやすく

中学数学 3年 式の計算9 乗法公式 2 例題解説と演習問題 Youtube

3

U9j580gf8iba369ji2w Xyz P 565

数学 乗法公式の整理 塾長の備忘録

乗法公式と問題練習 小学生 中学生の勉強

中3数学 第6講座 因数分解 学習塾サンクス ワン

乗法公式の問題 ａ ｂ ａ ｂ の展開を練習しよう 中学や高校の数学の計算問題

乗法公式の覚え方 4つの乗法公式を簡単に覚える方法 数学の面白いこと 役に立つことをまとめたサイト

Studydoctor根号 ルートと乗法公式を利用した計算 中３数学 Studydoctor

モノマナビ研究所

中３数学の基本問題プリント 問題と解答

数 乗法公式とその利用の定期テスト対策問題 解説付 Tekibo

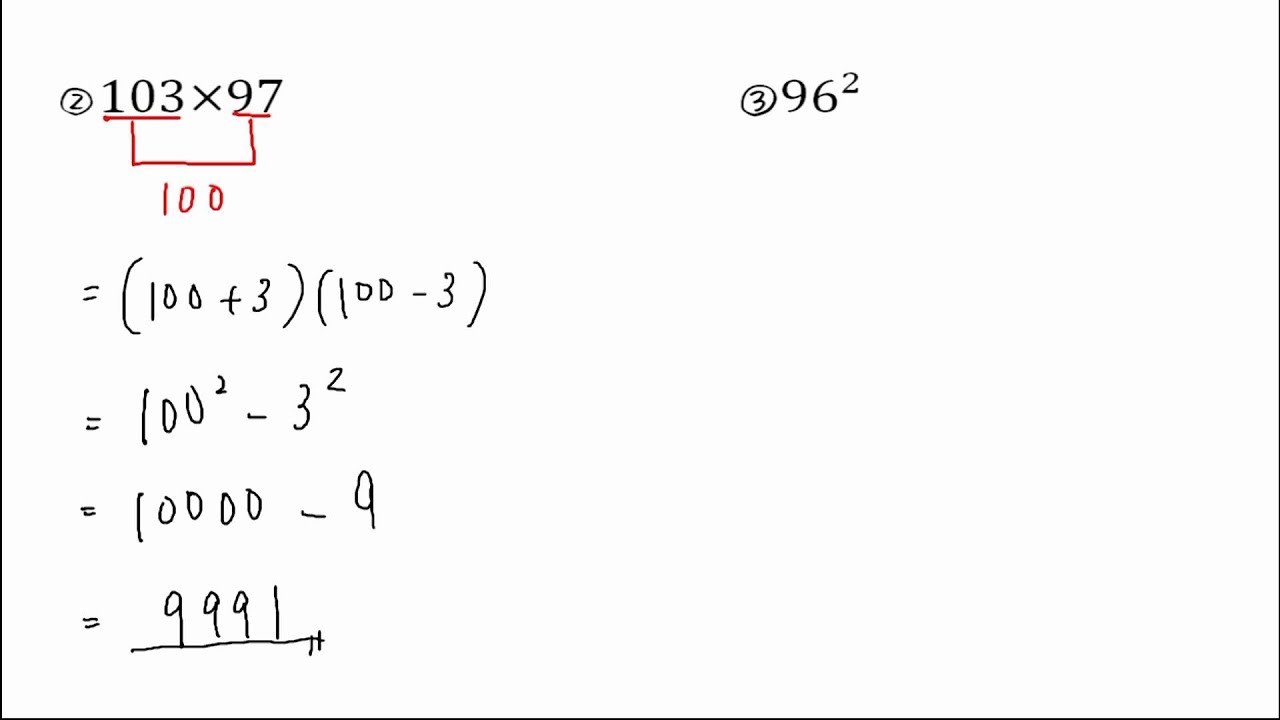
乗法公式を利用した計算 問題 Youtube

乗法公式とは 1分でわかる意味 公式の覚え方 問題 因数分解との関係

中学数学 多項式 の教え方 乗法公式

中学数学3年 展開と乗法公式 受験の月

中学数学 多項式 の教え方 展開の応用問題

Descubre Como Resolverlo En Qanda

中３ 展開と因数分解６ 乗法の公式 平方 予習 中学数学の勉強に

中学３年生 数学 多項式の乗法と除法 式の展開 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

Tossランド 乗法公式による展開 の基礎 基本

中3数学 01 10 乗法公式 X A X A 問題 Cmovie 教育に特化した無料動画サイト シームービー オンライン学習サイト

中学数学の乗法公式についての応用問題を下さい 中学の乗 Yahoo 知恵袋

数と式 整式の展開と乗法公式について 日々是鍛錬 ひびこれたんれん

Catatan Tentang 新中学3年生に向けて 数学乗法公式 Junior Clear

中学数学 多項式 の教え方 乗法公式

モノマナビ研究所

乗法公式 多項式の展開公式 の覚え方と使い方 数学fun

乗法公式の覚え方 4つの乗法公式を簡単に覚える方法 数学の面白いこと 役に立つことをまとめたサイト

Studydoctor乗法公式を利用する式の計算 中３数学 Studydoctor

Studydoctor乗法公式といろいろな問題 中３数学 Studydoctor

中３数学 平方根 ２９ 中学数学高校数学個別指導in山形市 数専ゼミ

中3数学の乗法公式で 値を求める問題の解き方が理解できないです 特 Yahoo 知恵袋

1

中3 中3数学 式の計算 多項式の計算 乗法公式 式の展開 中学生 Clear

乗法公式とは 1分でわかる意味 公式の覚え方 問題 因数分解との関係

Sukinakazu Net Takousiki Takousiki Pdf

乗法公式による式の展開と因数分解 中学数学の多項式計算 リョースケ大学

4つの乗法公式 教遊者

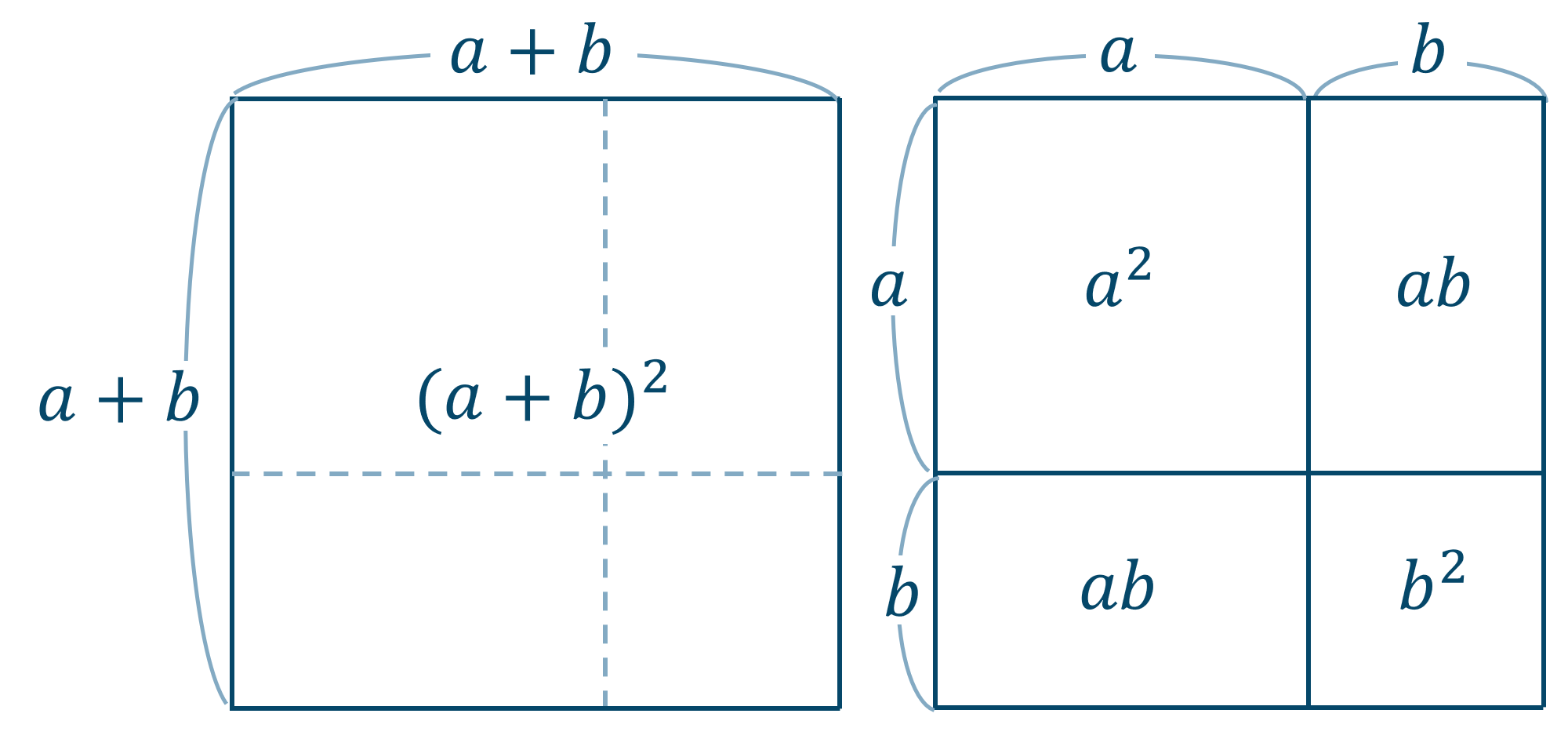
数学 ２次式の展開のコツと乗法公式 展開公式 ページ 2 教科書より詳しい高校数学

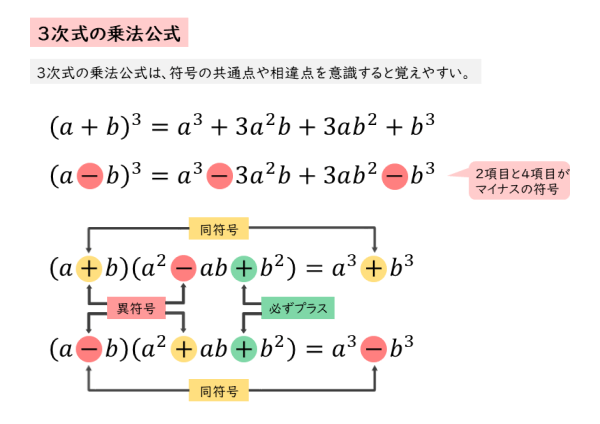
式と証明 ３次式の展開について 日々是鍛錬 ひびこれたんれん

因数分解の意味 問題の解き方 数学fun

中3数学の計算問題プリント 式の展開 と因数分解 桜花 現役バイト塾講師 Note

乗法公式 3の問題です 答えはx2 2x 48になると思 Yahoo 知恵袋

三乗の公式 展開と因数分解 高校生向け受験応援メディア 受験のミカタ

乗法公式

中３数学12 式の計算２ 乗法公式１ 標準問題 ヒント 302

乗法公式とは 1分でわかる意味 公式の覚え方 問題 因数分解との関係

3

乗法公式 無料で使える中学学習プリント

展開公式のまとめ 中学生や高校生の子はぜひ覚えておきたい 中学や高校の数学の計算問題

乗法公式による式の展開 効率良い復習 テクニックで勉強 テストが楽しくなるブログ

無料 中３数学 基本問題 問題プリント 302 式の計算２ 乗法 公式１

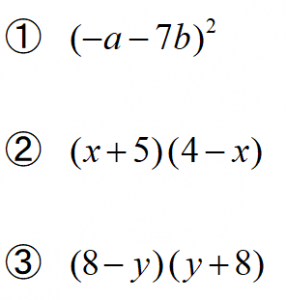
いろいろな多項式を展開してみよう 前編 インターネット家庭教師のアスミラ

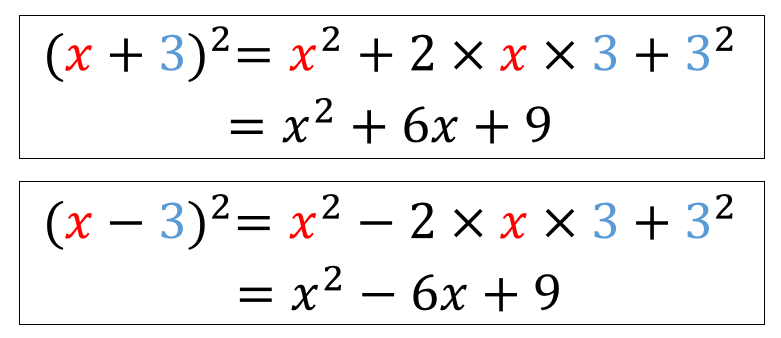
中3数学 展開の公式のやり方は 問題を使って徹底解説 数スタ

速くて簡単 乗法公式１ インターネット家庭教師のアスミラ

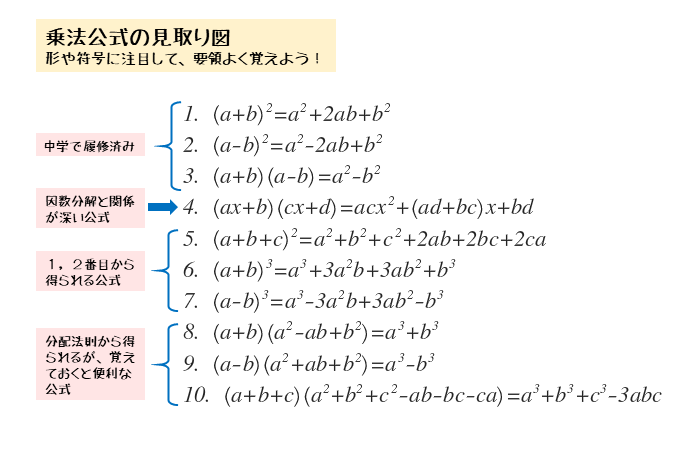
数と式 整式の展開に関する問題を解いてみよう 日々是鍛錬 ひびこれたんれん

式の展開 無料で使える中学学習プリント

中3数学 乗法の公式の定期テスト予想問題 Pikuu

中3 数学 乗法公式 まとめ 中学生 数学のノート Clear

至急お願い致します 中3 式の計算 乗法公式 式の展開 Clear

中3 中3数学 乗法公式の使い方 中学生 数学のノート Clear

乗法公式の覚え方 4つの乗法公式を簡単に覚える方法 数学の面白いこと 役に立つことをまとめたサイト

4つの乗法公式 教遊者

中３数学の基本問題プリント 問題と解答

ルート計算 展開公式をつかう3つの平方根問題の解き方 Qikeru 学びを楽しくわかりやすく

中3数学 01 8 乗法公式 X A 2 問題 Cmovie 教育に特化した無料動画サイト シームービー オンライン学習サイト

Youtube Lesson 中3 式の計算 3 乗法公式 桂坂数学教室

ルートの掛け算の問題 やり方は乗法とほとんど同じ 中学や高校の数学の計算問題

中学３年生 数学 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

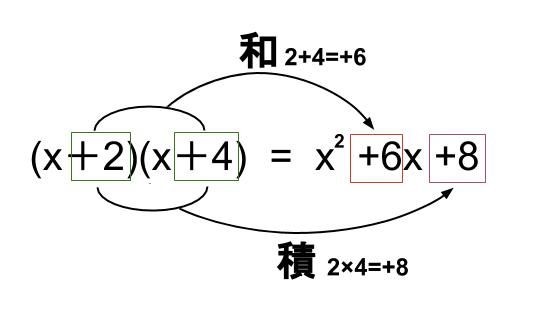
中学数学 式の展開 乗法公式 中学数学の無料オンライン学習サイトchu Su

式の展開 乗法公式を使った文字の置き換え問題の解き方とは 中学数学をはじめから分かりやすく

乗法公式を使えば 64 66 や 53 53は簡単に5秒以内で解くことができる 梅屋敷 Note

中3数学 展開の公式のやり方は 問題を使って徹底解説 数スタ

中3数学 展開の公式のやり方は 問題を使って徹底解説 数スタ